My insistence on stealing everything from every enemy came to an incredibly short end. Against some early monsters I put in 20 attempts at stealing with no success. Against one enemy I tried 40 times and didn't get it. I sort of wanted to just go until it worked, but I didn't know what the formula for success chance and I couldn't rule out the possibility is my chance of success was actually zero.
Fortunately for Final Fantasy games you can usually go to GameFAQs and find some pretty in depth guides to the numbers. In this case, the user instructrtrepe provides a guide to all of the games' algorithms. Given that most enemies in the game seemed to give up their steal item in a couple of attempts while others just didn't give it up at all, I thought there must be some bizarre formula. Maybe if I went up a level I'd have more luck, or maybe the chance of stealing was just fixed at 40%.
It's that second one.
For a moment I was going to take this as a lesson in not being fooled by randomness, but look at those numbers again. Against three or maybe four enemies I tried 20 times. Against one enemy I tried 40 times. Forty consecutive 60% rolls is starting to raise questions.
But what questions ought it raise? First of all, let's do away with the very common logical fallacy that people use to argue that there is a god. Statement A is that stealing has a fixed 40% success rate. Statement B is that I stole 40 times in a row from an enemy and failed every time. B given A is only about one in a billion. B is true. That allows me to conclude absolutely nothing about A. Basically, you cannot get A given B from B given A, you need an additional piece of information. You're very unlikely to win the lottery given that the sun came up in the morning, but someone wins the lottery every day and the sun keeps coming up.
On the other hand you can say something about the probability of A given B if you have B given A and the probability of A and B independently. Bayes Theorem says:
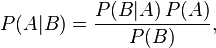
and I know that P(B|A) is about one in a billion. In order to get P(A|B) I'd need to know what P(A) and P(B) are. Do I have any idea? Given that I got the 20 in a row result several times, I'm guessing off the top of my head that P(B) isn't itself something like one in a million. P(A) is harder to get a feel for: First of all, GameFAQs is a place people go for this sort of detailed information in text form for final fantasy games, or at least it replicates the information sources people go to. Second, this would be a giant glaring omission - to think I'm the only person who noticed that the chance of stealing from some monsters was not 40% at all would be a bit like thinking I was the only one who noticed that ISIS was marching in the London pride parade. Odds are that the guide wasn't wrong but that I was misunderstanding what the guide said.
Here is the algorithm for determining stealing: First, set chance of success at 40%. Next apply modifier to steal success. Get a random number from 0 to 99. If the number is greater than or equal to the success chance then stop. If an item has already been stolen from the target then stop. Get another random number from 0 to 255. If that number is less than 10 get a rare item. If that number is greater than or equal to 10 get a common item.
So obviously something happened in that "apply modifier to steal success" step. But it turns out that step is as follows:
If the Attacker is wearer a Thief Glove, Hit% = Hit% * 2
No help there. What could be going on?
What's missing is a second algorithm that determines which message to provide to the player. Clearly, if an item was generated then it provides a message saying what item was stolen. But if no item is generated then it can either say, "Nothing to steal" or "Couldn't steal".
Note that the choice of message is not generated by the termination point of the steal algorithm itself. It checks if you miss your steal attempt before checking if an item has already been stolen. So "Nothing to steal" could mean that an item had already been stolen, or it could mean that there was no item to steal in the first place - that is, the monster has nothing for both its common and its rare steal. That message can be provided whether you hit or missed.
But what about monsters that have nothing for a common steal but have something for their rare steal? Yes, those exist on the list of monsters. It may go through the algorithm, get a hit, and still provide no result. But the monster does have something that could be stolen, so it says "Couldn't steal" instead of "Nothing to steal".
The chance of a rare steal is 10 in 256. Since the chance to hit is 40%, the chance to hit and get a rare steal is a neat 1 in 64. So if a monster has a rare steal but no common one - giving you a 1 in 64 chance of stealing something - you'll get the same message as if the monster has both a rare and a common steal - giving you a 40% chance of stealing something.
This isn't very helpful feedback from the game, and it appears to run through nearly every stage of the game. Fortunately the difference between 4 in 10 and 1 in 64 is pretty easy to detect by experimentation so it isn't necessary to constantly check the guide. Unfortunately this scheme doesn't guarantee that the item you steal will be worth it. Those monsters I was failing to steal from in the first cave could have yielded potions if I had stuck with it.
What's missing is a second algorithm that determines which message to provide to the player. Clearly, if an item was generated then it provides a message saying what item was stolen. But if no item is generated then it can either say, "Nothing to steal" or "Couldn't steal".
Note that the choice of message is not generated by the termination point of the steal algorithm itself. It checks if you miss your steal attempt before checking if an item has already been stolen. So "Nothing to steal" could mean that an item had already been stolen, or it could mean that there was no item to steal in the first place - that is, the monster has nothing for both its common and its rare steal. That message can be provided whether you hit or missed.
But what about monsters that have nothing for a common steal but have something for their rare steal? Yes, those exist on the list of monsters. It may go through the algorithm, get a hit, and still provide no result. But the monster does have something that could be stolen, so it says "Couldn't steal" instead of "Nothing to steal".
The chance of a rare steal is 10 in 256. Since the chance to hit is 40%, the chance to hit and get a rare steal is a neat 1 in 64. So if a monster has a rare steal but no common one - giving you a 1 in 64 chance of stealing something - you'll get the same message as if the monster has both a rare and a common steal - giving you a 40% chance of stealing something.
This isn't very helpful feedback from the game, and it appears to run through nearly every stage of the game. Fortunately the difference between 4 in 10 and 1 in 64 is pretty easy to detect by experimentation so it isn't necessary to constantly check the guide. Unfortunately this scheme doesn't guarantee that the item you steal will be worth it. Those monsters I was failing to steal from in the first cave could have yielded potions if I had stuck with it.


No comments:
Post a Comment